今回はH28年第8問の乗数理論の問題を解説します。
H28 経済学 第8問
財市場における総需要Aが以下のように定式化されている。
A = C + I + G
【C:消費、I:投資、G:政府支出】
ここで、消費 C を以下のように定式化する。
C = C0 + cY
【Y:所得、C0:独立消費、c:限界消費性向(0 < c < 1)】
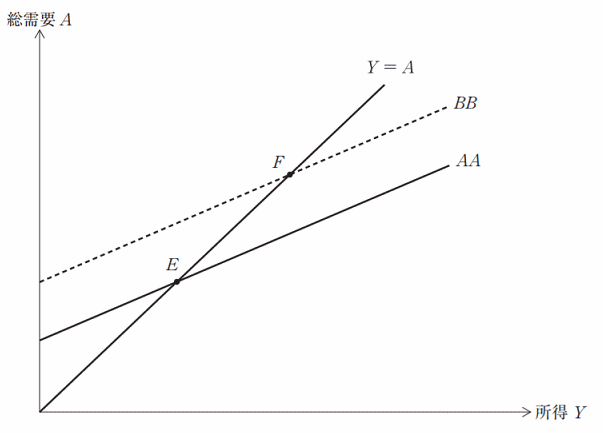
このとき、総需要は A = C0 + cY + I + G と書き改めることができ、総需要線として下図の実線AAのように描くことができる。
下図の45度線(Y = A)は、財市場で需要と供給が一致する均衡条件を示しており、実線AAとの交点Eによって均衡所得が与えられる。なお、簡便化のために、限界消費性向 cは 0.8であると仮定する。
このような状況をもとに、下記の設問に答えよ。
(設問1)
政府支出乗数と租税乗数の値として、最も適切なものはどれか。
ア 政府支出乗数と租税乗数はともに4である。
イ 政府支出乗数と租税乗数はともに5である。
ウ 政府支出乗数は5、租税乗数は4である。
エ 政府支出乗数は8、租税乗数は2である。
(設問2)
いま、他の条件を一定として、I + G の値が外生的に5増加し、図中の実線AAが破線 BBへシフトし、点Fで均衡するものとする。このとき、均衡所得の変化量として、最も適切なものはどれか。
ア 4
イ 10
ウ 25
エ 40
解説
それではまずは設問1を見てみましょう。
政府支出乗数と租税乗数を求めます。
総需要は A = C + I + G で、Y = A なので、
Y = C + I + G となります。
この問題では租税乗数を問われているため、
C = C0 + c(Y - T) とすると、
Y = C0 + c(Y - T) + I + G と表せます。
これをYについて解くと
(1 - c)Y = C0 - cT + I + G
Y = 1/(1 - c){C0 - cT + I + G} ・・・①
と表せ、
①式のG、Tの項から政府支出乗数は1/(1 - c)、租税乗数は-c/(1 - c)となります。
c = 0.8ですので、
政府支出乗数は1/(1 - 0.8) = 5、租税乗数は-0.8/(1 - 0.8) = – 4となります。
これより、正解は選択肢ウとなります。
次に設問2を見てみます。
政府支出乗数や租税乗数と同じ考え方で、①式のI + Gの項から、
I + Gが1変化すると、Yは1/(1 - c)変化することがわかります。
c = 0.8ですので、
I + Gが1変化すると、Yは 1/(1 - 0.8) = 5 変化するため、
I + Gが5増加すると、Yは5 × 5 = 25 増加します。
よって、正解は選択肢ウとなります。
Amazonベストセラー1位獲得
一目でわかる!覚えてしまう!中小企業診断士一発合格まとめシート
好評発売中
後編は1/21~発売予定!
—–