今回はH24年第16問の費用関数の問題について解説します。
H24 経済学 第16問
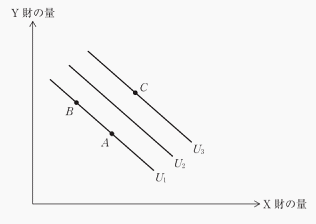
下図は、X財とY財に対するある個人の無差別曲線(U1,U2,U3)を描いたものである。U1,U2,U3は直線であるものとし、A点とB点は無差別曲線U1上にあり、C 点は無差別曲線U3上にある。
この図の説明として最も適切なものを下記の解答群から選べ。
[解答群]
ア 効用の不飽和性が成り立つ場合、A点とC点の効用水準は等しい。
イ これらの無差別曲線の限界代替率は逓減している。
ウ これらの無差別曲線は、2つの財が完全代替財であることを意味している。
エ これらの無差別曲線は、2つの財が完全補完財であることを意味している。
オ 無差別曲線U1上でA点から得られる効用水準は、B点から得られる効用水
準よりも高い。
解説
それでは早速各選択肢を見ていきましょう。
選択肢アは、「A点とC点の効用水準は等しい」とありますが、A点とC点は別の無差別曲線上にあるので、効用は等しくありません。
なお「効用の不飽和性」というのは、ざっくり言うと「欲求には制限がない」ことを想定したもので、X財かY財いずれかの消費量が増えると必ず効用は増える性質を表しています。
選択肢イについて、無差別曲線は直線であると問題文中に書いてありますので、その傾きである限界代替率は一定です。そのため、この選択肢は×となります。
選択肢ウはその通りで、無差別曲線が右下がりの直線で示される財は例えば500円玉と100円玉のような完全代替材です。
選択肢エについて、上記の説明の通り、2つの財は完全代替材ですので×です。
選択肢オについて、A点とB点は同じ無差別曲線上にあるので×です。
以上から正解は選択肢ウとなります。
Amazonベストセラー1位獲得
一目でわかる!覚えてしまう!中小企業診断士一発合格まとめシート
好評発売中
—–