今日は、経済学のH28 第21問について解説します。
H28 経済学 第21問
いま、1つの要素を用いて1つの生産財を生産するものとする。要素投入量をxとし、その単位当たりの購入価格をwとする。また、生産財の生産量をyとし、その単位当たりの販売価格をpとする。このとき利潤πは、π=py-wxと書くことができ、y=π/p + wx/pと書き直すこともできる。
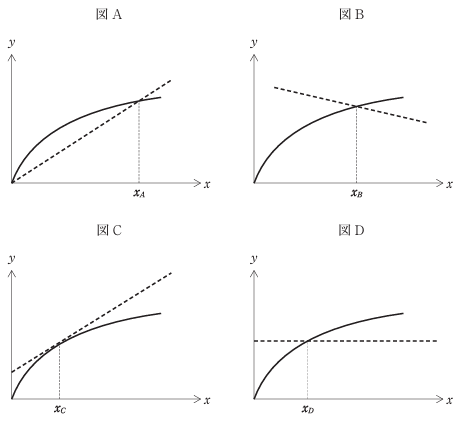
以下にある4つの図は、縦軸を生産量、横軸を要素投入量として、一般的な生産関数を実線で描き、上記で導いたy=π/p + wx/pを 破線で書き加えたものである。
企業の利潤最大化が実現することを示す図として、最も適切なものを下記の解答群から選べ。
[解答群]
ア 図A
イ 図B
ウ 図C
エ 図D
解説
生産関数に関する問題です。
まとめシートでは、以下の通り解説しています。
本問に出てくる変数x、y、w、p、πは全て正の整数となるため、y=π/p + wx/pを表すグラフは、切片(y軸との交点)がプラスで、傾きが正(右上がり)となります。
これを満たす破線が書いてある図は、図Cのみとなります。
利潤が最大となるのはpy=wのときです。この式の両辺をpで割ると、y=w/pとなり、本文中のy=π/p + wx/pの傾きと同じであることがわかります。この関数と生産関数の交点で、生産量と利潤が均衡します。よって、y=π/p + wx/pと生産関数が書いてある図=企業の利潤最大化が実現することを示す図となります。
以上から、正解は選択肢ウとなります。
◆ブログ村参加しています◆
気に入っていただけたら、クリックお願いします!
関連教材で学習効率アップ!