今日は経済学のH25第13問について解説します。
H25 経済学 第13問
人生を若年期(期間1)と老年期(期間2)とに分ける。期間i(i=1,2) における消費をCi、所得をYi、利子率をrとする。貯蓄と借入(負の貯蓄)は若年期においてのみ行われ、老年期を終える時点では貯蓄も借入も残さないものとする。
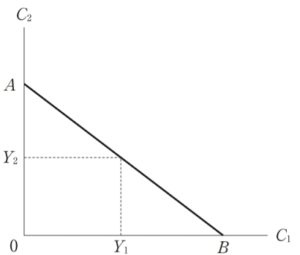
下図は、横軸に若年期の消費(C1)を、縦軸に老年期の消費(C2)をとり、若年期と老年期の所得を所与として、貯蓄や借入に制約がない場合に選択可能な若年期と老年期の消費の組み合わせを右下がりの直線ABで表している。
直線ABの形状の説明として、最も適切なものを下記の解答群から選べ。
[解答群]
ア 縦軸の切片が Y1+(1+r)Y2で、傾きが -(1+r) の直線。
イ 縦軸の切片が Y1+(1+r ) Y2 で、傾きが -1/(1+r)の直線。
ウ 縦軸の切片が (1+r) Y1 + Y2 で、傾きが -(1+r)の直線。
エ 縦軸の切片が (1+r) Y1 + Y2 で、傾きが -1/(1+r)の直線。
解説
今回の問題は異時点間の消費と貯蓄に関する問題です。
一見難しそうに見えますが、経済学の知識がなくても、一次関数の式とグラフの関係がわかれば、対応できなくはない問題です。
それでは早速考えていきましょう。
問題文を踏まえると、ある時点(Y1, Y2)では、若年期の消費がY1、老年期の消費がY2ということがわかります。
一次関数の切片と傾きは、2点の座標がわかれば求めることができますので、もう1点の座標で求められそうなところを考えます。
そういった場合、極端な例の場合だと考えやすいので、C1=0またはC2=0の点の座標を求められないかと考えます。
C1=0のときというのは、若年期は全く消費せず、老年期に若年期で貯めたお金まで全部使い切る場合で、C2=0のときというのは、若年期に老年期の所得の分まで借金しまくって、老後は全くお金が使えない場合です。
両者を比較すると、どちらかというと借金よりは貯蓄の方がシンプルに考えられそうですし、ついでに切片も求められるので、若年期に全貯蓄するC1=0の場合で考えることとします。
ある時点では若年期の消費がY1、老年期の消費がY2だったということは、
もし若年期に全く消費をしなかった場合は、老年期の消費Y2に加えて、若年期で消費していたはずのY1を使わずに貯蓄していた場合と考えることができます。
すると、老年期に使えるお金は、Y2に加えて、Y1と、Y1を貯蓄していたことによって得られる利子 であると考えることができます。
Y1を貯蓄していたことによって得られる利子は、利子率がrとされているのでrY1、これらをすべて足すと
C1=0のときのC2の値は
Y2+Y1+rY1 つまり、 (1+r) Y1 + Y2 となります。
これは切片でもありますので、正解は選択肢ウまたはエに絞ることができます。
直線上の2点がわかったので、あとは傾きを求めます。
直線の傾きは、 C2の増加量/C1の増加量 で求めることができますので、
((1+r) Y1 + Y2-Y2)/(0-Y1) で求めることができ、これを計算すると
=(1+r) Y1 /(-Y1)=-(1+r)
となります。
以上から、正解は選択肢ウとなります。
◆ブログ村参加しています◆
気に入っていただけたら、クリックお願いします!
2020年度版まとめシート(前編、後編)
Amazon&書店にて好評発売中!