今日は運営管理のR2第11問について解説します。
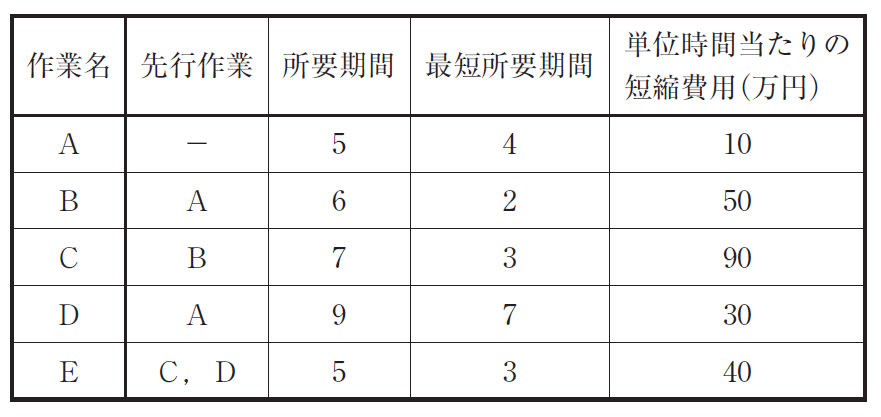
下表は、あるプロジェクト業務を行う際の各作業の要件を示している。CPM(Critical Path Method)を適用して、最短プロジェクト遂行期間となる条件を達成したときの最小費用として、最も適切なものを下記の解答群から選べ(単位:万円)。
〔解答群〕
ア 440
イ 510
ウ 530
エ 610
オ 710
解説
CPM(Critical Path Method)に関する問題です。設問は「最短プロジェクト遂行期間となる条件を達成したときの最小費用」ですから、作業の先行関係と所要期間の表からPERT図を作成し、クリティカルパス上にある作業を求め、それを短縮した場合の費用を求めていきます。
最初に通常の所要期間に基づいて、アローダイヤグラム(PERT図)を書いてみます。
所要期間は23、クリティカルパスはA→B→C→Eであることがわかります。
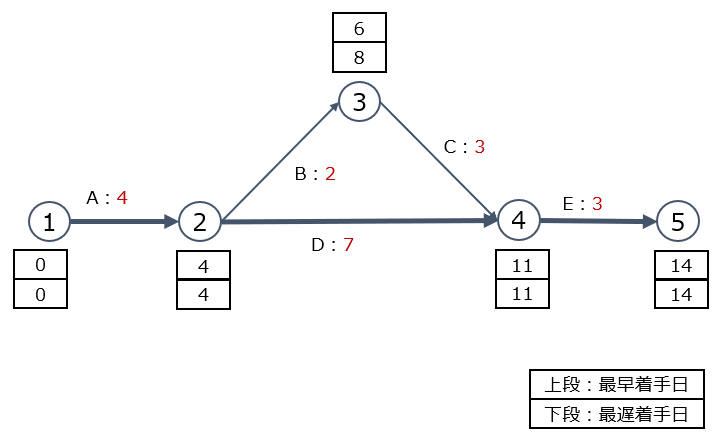
次に最短所要期間に基づいて、アローダイヤグラム(PERT図)を書いてみます。
所要期間は14まで短縮でき、クリティカルパスはA→D→Eに移ることが確認できます。
この時点で、クリティカルパス上にある作業であるA、D、Eについては最短所要期間まで短縮を行わなければなりませんので、
作業A:5→4で10万円
作業D:9→7で30×2=60万円
作業E:5→3で40×2=80万円
の費用が必要になることがわかります。
ここで作業B、作業Cに着目してみると、クリティカルパスに対して2の余裕があることがわかりますので、それぞれを最短所要期間まで短縮しなくてもよいことがわかります。
単位時間当たりの短縮費用は、作業Bが50万円、作業Cが90万円ですから、費用の高い作業Cの短縮期間を2少なくして7→5とすれば費用が最小になることがわかります。
アローダイアグラム(PERT図)を見てみると、すべての作業経路がクリティカルパスになっている(=どこにも余裕がない)状態であることがわかります。
この時の作業B、作業Cの所要期間は、
作業B:6→2で50×4=200万円
作業C:7→5で90×2=180万円
となり、期間短縮に必要な短縮費用の合計は、
10(作業A)+ 200(作業B)+ 180(作業C)+ 60(作業D)+ 80(作業E) = 530万円となりますので、正解は選択肢ウとなります。